Appearance
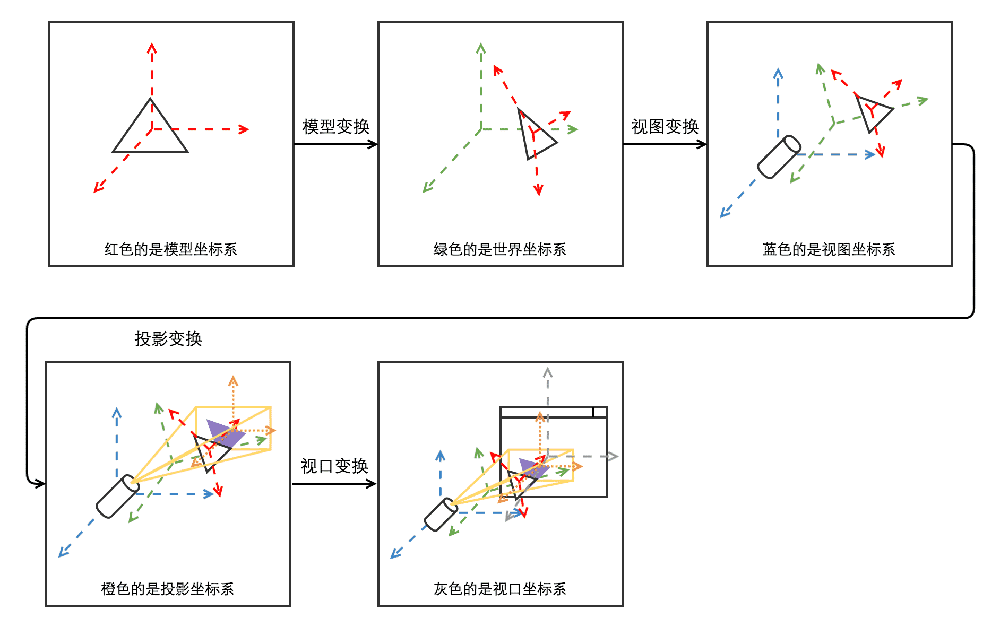
图解
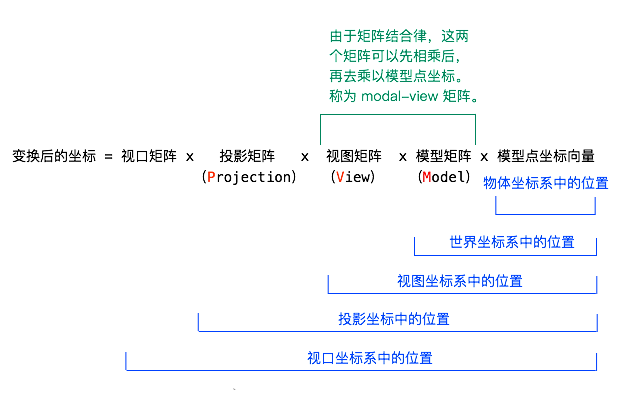 又称为 MVP 矩阵
又称为 MVP 矩阵
从逻辑上来说,是先把模型点坐标向量乘以模型矩阵,然后乘以视图矩阵,然后乘以投影矩阵,然后乘以视口矩阵的。所以顺序的确是 MVP。
javascript
model world view view projection projection viewport
模型坐标---(模型变换)--->世界坐标---(视图变换)--->视图坐标--->(投影变换)--->投影坐标---(视口变换)--->视口坐标
--------------------------------------------------------------------------------------------------------------
模型变换(Model Transformation)
模型矩阵 x 模型点坐标向量,得到世界坐标
视图变换(View Transformation)
将世界坐标系中的物体转换到相机坐标系(也称为视图坐标系)。这个转换基于相机的位置和朝向,确保了从相机的视角观察场景。
视图变换的步骤:
1、相机位置和朝向(相机在世界坐标系中有一个位置,通常表示为CameraPosition;相机有一个朝向,这通常由一个前向向量Forward,一个上向量Up和一个右向量Right定义。)
2、视图矩阵的构建(视图矩阵(View Matrix)是一个4x4矩阵,用于将世界坐标转换为相机坐标;这个矩阵通常通过相机的位置和朝向向量计算得出。它包含了相机的平移和旋转信息。)
3、视图矩阵的计算(第一步,相机到世界,首先计算一个从相机指向世界的矩阵,这涉及到相机的逆旋转和平移。第二步,构建矩阵,使用相机的位置和朝向向量构建视图矩阵。)
投影变换(Projection Transformation)
投影变换是将视图坐标转换为投影坐标的过程。这个过程涉及到构建一个投影矩阵,并将视图坐标中的每个顶点乘以这个矩阵。
投影变换的目的是:
1、透视投影:模拟人眼观察世界的方式,远处的物体看起来更小,近处的物体看起来更大。这通过透视除法实现,其中x、y、z坐标被除以w坐标(透视除法)。
2、平行投影:保持物体的尺寸不变,无论它们离相机的距离如何。这通常用于技术绘图或一些特定的视觉效果。
视口变换(Viewport Transformation)
它发生在投影变换之后,负责将投影坐标转换为屏幕上的实际像素坐标。
这个过程包括两个主要步骤:缩放变换和平移变换
1、缩放变换:缩放变换的目的是将标准立方体(通常是[-1, 1]³)的x和y轴长度分别缩放到屏幕的宽度和高度。由于-1到1的距离是2,所以缩放长度分别为屏幕宽度的一半和高度的一半。
2、平移变换:平移变换将标准立方体的中点从原点平移到屏幕中心。在屏幕坐标系中,屏幕的中心通常是(width/2, height/2),其中width和height是屏幕的宽度和高度。
视口变换的结果就是将3D场景中的物体映射到2D屏幕上的特定区域。这个映射过程确保了渲染的图像能够正确地显示在屏幕上,并且与显示设备的像素对应起来。
视口变换完成后,物体到屏幕的所有变换都完成了,接下来的步骤是光栅化,即将这些结果信息变成屏幕上的像素。光栅化是将几何图形转换为像素的过程,这是渲染管线中的下一步。
总结来说,视口变换是将投影坐标(通常是归一化的设备坐标,范围在[-1, 1]之间)转换为屏幕上的实际像素坐标的过程,它定义了屏幕上的显示区域,并确定了顶点屏幕坐标的变换方式。
--------------------------------------------------------------------------------------------------------------
世界坐标(World Coordinates)
指的是一个物体在3D世界空间中的位置和方向,这个空间是相对于整个场景或宇宙的全局坐标系
World Position = Model Matrix × Local Position
视图坐标(View Coordinates)
视图坐标是经过视图变换后的坐标系,它代表了从相机视角观察到的3D世界。
在这个坐标系中:
1、位置:物体的位置是相对于相机的位置来确定的。如果相机位于原点并朝向负z轴,那么正z轴方向的物体会远离相机,而负z轴方向的物体会靠近相机。
2、方向:物体的方向也是相对于相机的朝向来确定的。相机的前向向量通常指向负z轴,上向量指向y轴的正方向。
投影坐标(Projective Coordinates)
投影坐标是经过投影变换后的坐标系,它们位于裁剪空间(Clipping Space)中。
在这个坐标系中:
1、坐标范围:坐标通常位于[-1, 1]的范围内,x和y坐标表示水平和垂直位置,z坐标表示深度(从相机到物体的距离)。
2、透视除法:对于透视投影,投影坐标需要进行透视除法,即将x、y、z坐标除以w坐标,以将坐标归一化到[-1, 1]的范围内。
3、裁剪:裁剪操作会移除超出[-1, 1]范围的坐标,这些坐标不会被渲染到屏幕上。
视口坐标(Viewport Coordinates)
1、视口坐标的特点:
像素单位:视口坐标是以像素为单位的,它们直接对应于屏幕上的像素位置。
坐标范围:视口坐标的范围取决于视口的大小。如果视口的宽度和高度分别是width和height,那么视口坐标的x范围是从0到width-1,y范围是从0到height-1。
与设备相关:视口坐标是与具体显示设备相关的,它们考虑了屏幕的分辨率和像素密度。
2、视口坐标的转换过程:
归一化设备坐标(NDC):在视口变换之前,坐标通常处于归一化设备坐标(NDC)中,其范围是[-1, 1]。
视口变换:视口变换将NDC坐标转换为视口坐标。这个转换包括缩放和偏移操作。缩放:将NDC坐标从[-1, 1]映射到视口的宽度和高度。偏移:将坐标平移,使得视口的左下角成为原点。
裁剪:在转换过程中,任何超出视口范围的坐标都会被裁剪掉,不会在屏幕上显示。
3、视口坐标的应用:
光栅化:视口坐标用于光栅化过程,即将几何图形转换为屏幕上的像素。光栅化器使用视口坐标来确定哪些像素需要被填充颜色。
用户交互:在处理用户输入(如鼠标点击或触摸)时,视口坐标用于将屏幕坐标转换为世界坐标或视图坐标,以便确定用户交互的具体位置。
--------------------------------------------------------------------------------------------------------------
projection view modelMatrix position
变换后的坐标 = 视口矩阵 x 投影矩阵 x 视图矩阵 x 模型矩阵 x 模型点坐标向量
mvp
模型视图矩阵-------->由于矩阵结合律,view和model可以先相乘后,再乘以模型点坐标向量,称为model-view矩阵
--------------------------------------------------------------------------------------------------------------
模型点坐标向量 (Model Point Coordinates):
这是3D模型中顶点的原始坐标。这些坐标是相对于模型自身的局部坐标系的。(一般都是使用position.xyz)
模型矩阵 (Model Matrix):
模型矩阵用于将模型的局部坐标转换到世界坐标系中。这个矩阵包含了模型的位置、旋转和缩放信息。通过乘以模型矩阵,可以将模型放置在世界空间中的任何位置。
视图矩阵 (View Matrix):
视图矩阵代表了相机的位置和朝向。它将世界坐标转换到相机坐标系中。这个矩阵通常包含了相机的位置(负值表示相机看向的方向)和相机的朝向(旋转)。
投影矩阵 (Projection Matrix):
投影矩阵定义了相机的投影方式,比如透视投影或正交投影。它将相机坐标系中的坐标转换到裁剪坐标系中。裁剪坐标系是一个标准化的坐标系,其中x、y、z坐标的范围通常是-1到1。
视口矩阵 (Viewport Matrix):
视口矩阵将裁剪坐标系中的坐标转换到屏幕坐标系中。这个矩阵定义了屏幕空间的尺寸和位置,它将裁剪坐标映射到窗口或视口的像素坐标上。一个物体的三维坐标向量(position),乘以模型视图矩阵(modelView)后,能够得到它在视图坐标系中的位置,也就是它相对于摄像机的坐标位置。
以下这个是获取到 xyz 的位置
javascript
vec4(position, 1.0): 将vec3类型的position转换为vec4类型,添加一个额外的w分量,设置为1.0。这是为了与4x4模型矩阵兼容
modelMatrix * vec4(position, 1.0): 将模型矩阵与扩展的顶点位置向量相乘,将顶点从局部坐标转换到世界坐标
世界坐标:指的是一个物体在3D世界空间中的位置和方向,这个空间是相对于整个场景或宇宙的全局坐标系
v_position = vec3(modelMatrix * vec4(position, 1.0))
f_position = (modelMatrix * vec4(position, 1.0)).xyz
v_position.xyz === f_positionModelMatrix(模型矩阵)、ModelViewMatrix(模型视图矩阵)、ProjectionMatrix(投影矩阵)、NormalMatrix(正规矩阵)
position 是顶点在物体坐标系(而不是世界坐标系)中的位置
意味着,一个正方体位于世界坐标系的(2, 0, 0)与位于(0, 0, 0)将不会改变任何顶点的 position
position 是相对于正方体的锚点而言的
因此,顶点着色器的作用就是将 uv 信息传递到片元着色器中,并按默认的方式计算顶点位置
javascript
gl_Position = projectionMatrix * modelViewMatrix * vec4(position, 1.0)uniform mat4 world;
uniform mat4 worldViewProjection;
| 名字 | 含义 | 在 CPU 端通常怎么算 | 在着色器里起什么作用 |
|---|---|---|---|
| world | 把顶点从“模型局部空间”转到“世界空间” | 由场景图/引擎根据模型的缩放-旋转-平移直接算出,每帧可能变一次 | 当你需要在世界坐标系下做计算(光照、法线变换、环境反射、世界位置采样等)时才用它:vec4 worldPos = world * vec4(position, 1.0); |
| worldViewProjection | 把顶点一次性从“模型局部空间”转到“裁剪空间”(齐次裁剪坐标) | 由 CPU 先把 world、view、projection 三个矩阵乘在一起,再传进来:wvp = P * V * W | 只做顶点最终输出,不参与光照:gl_Position = worldViewProjection * vec4(position, 1.0); |
一句话区别:
world 只负责“模型→世界”,给你在世界坐标系里干活用;
worldViewProjection 是“模型→世界→视图→投影”的合并捷径,唯一目的就是快速算出 gl_Position,让 GPU 走后续裁剪-光栅流程。
因此:
- 需要世界坐标位置/法线/向量 → 用
world; - 只想把顶点甩到裁剪空间 → 用
worldViewProjection,省掉在 VS 里再乘三遍矩阵。