Appearance
正fft算法
······ 复数乘法
javascript
(a+bi)×(c+di) = ac + adi + bci + bdi^2
进一步化简,考虑到i^2 = -1,得到:
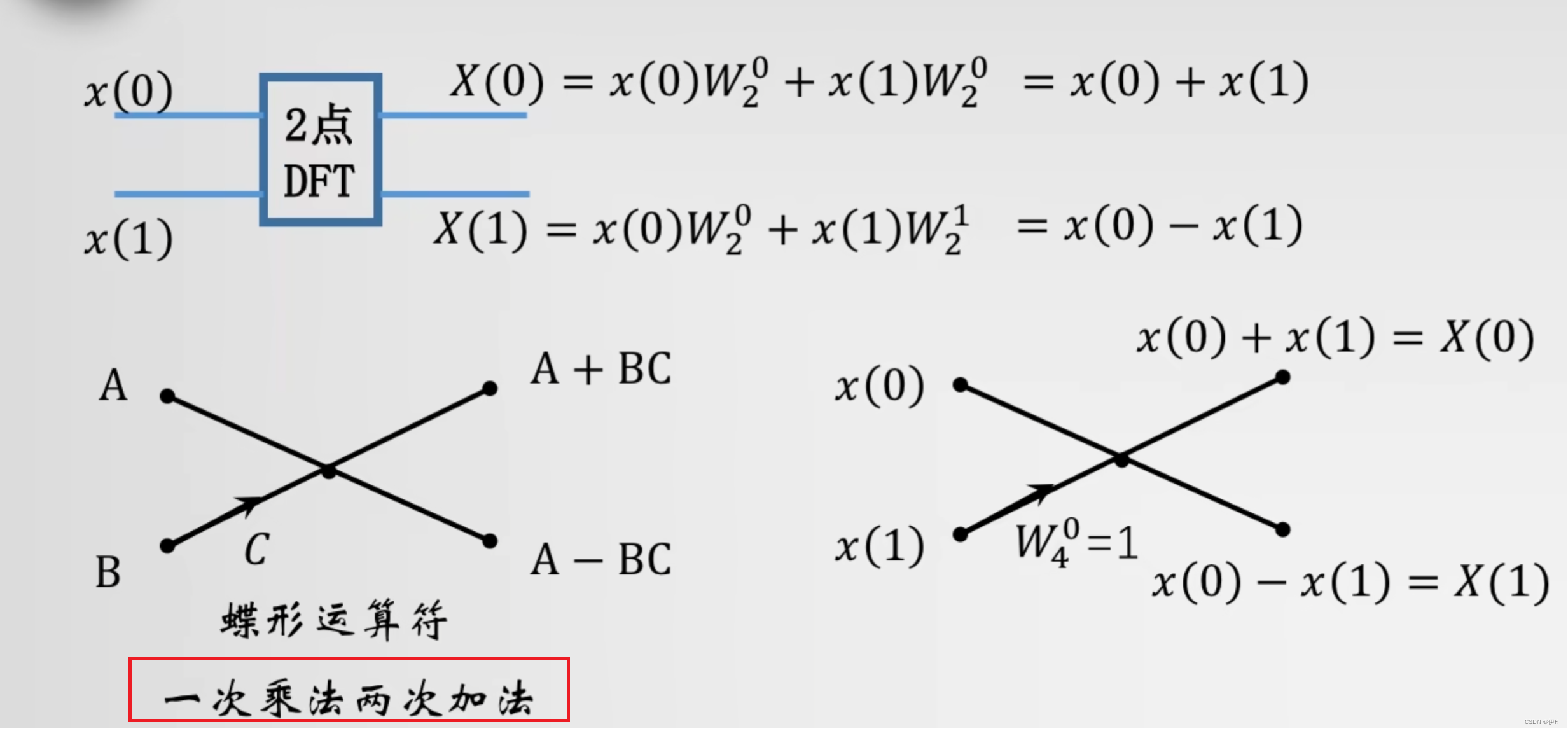
ac + adi + bci - bd = (ac - bd) + (ad + bc)i取W的原理
javascript
/**
* w的取值计算
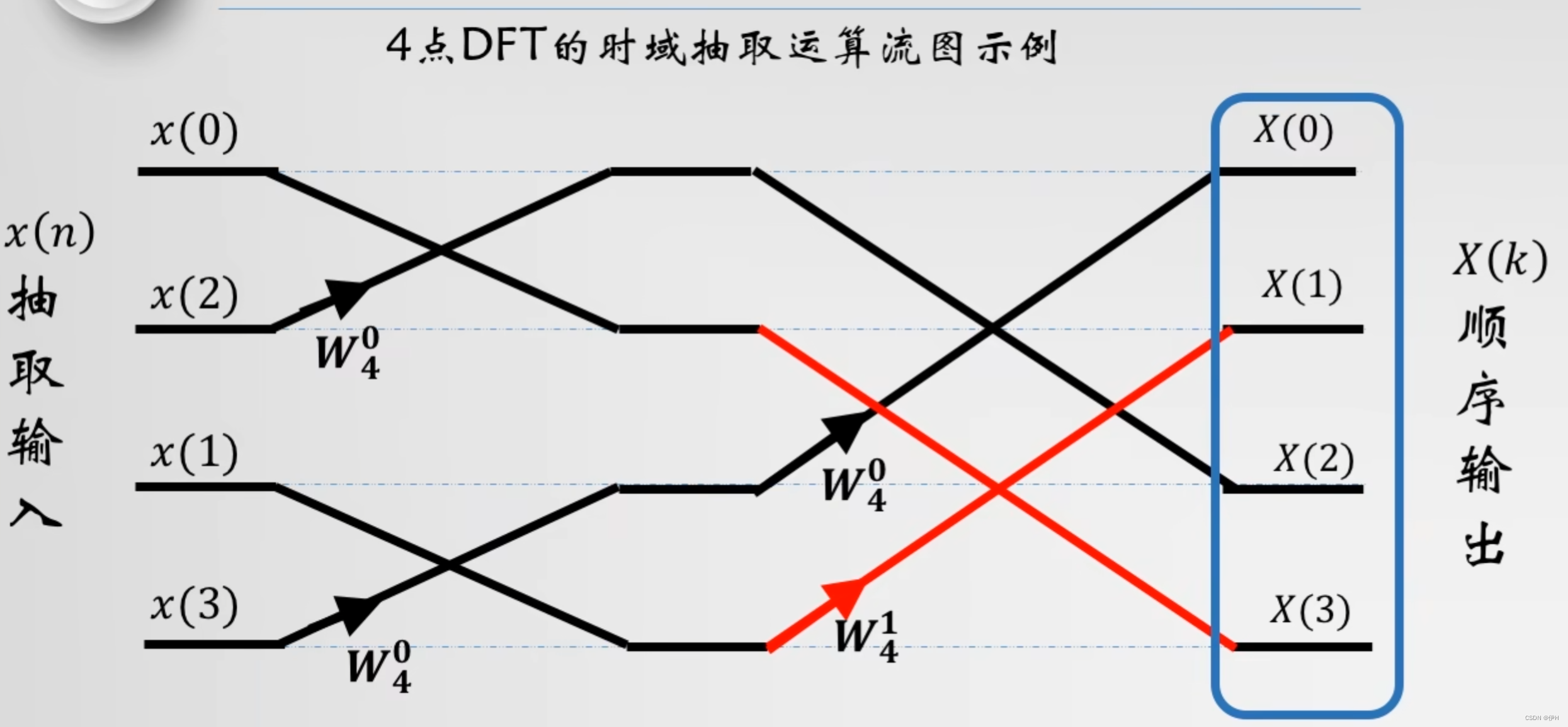
* W_N_k 中,k 的取值是: J * 2^(M - L)【M 是log2*(8) = 3、L 是从1开始的第几轮、J 是每块大小中从0开始循环的值】
*/
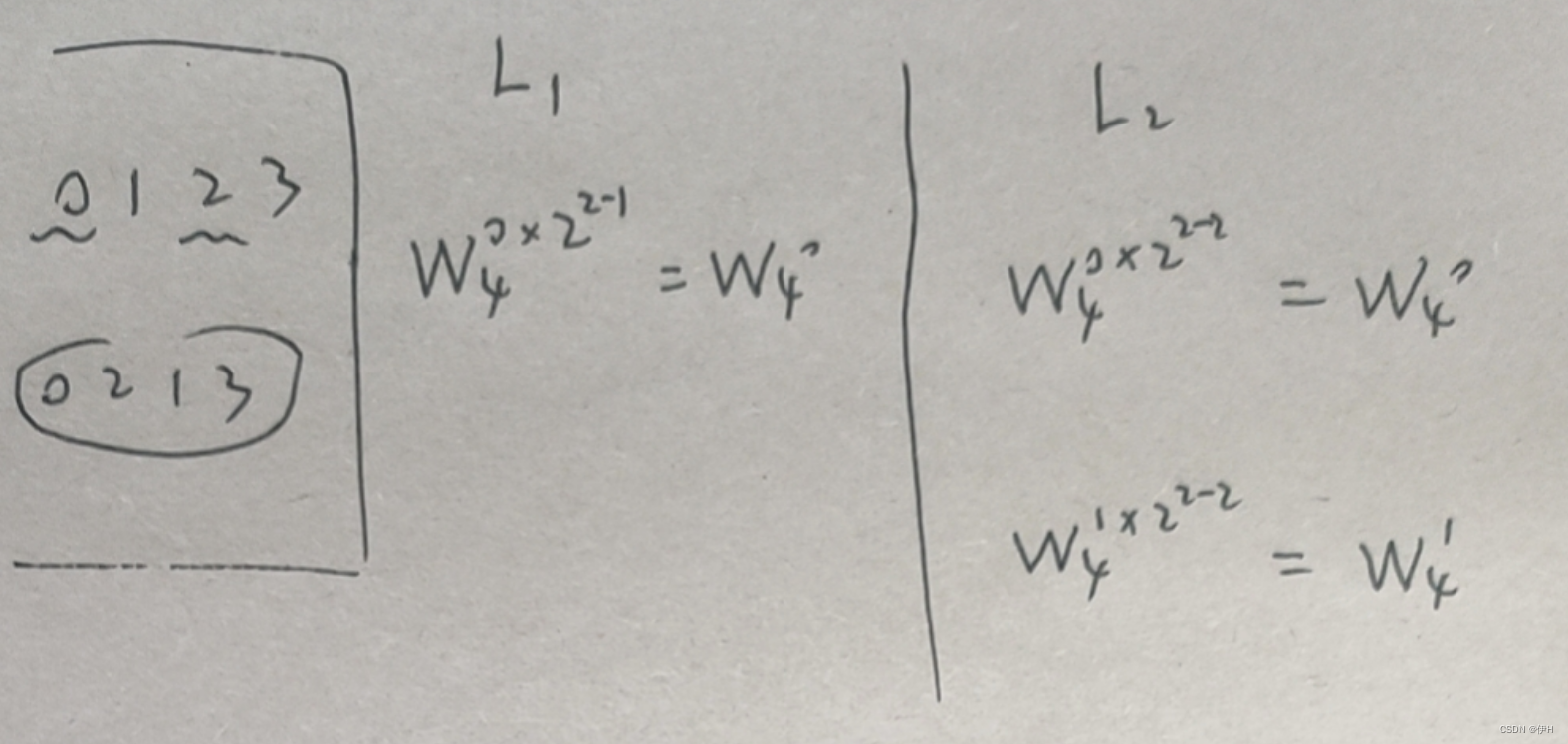
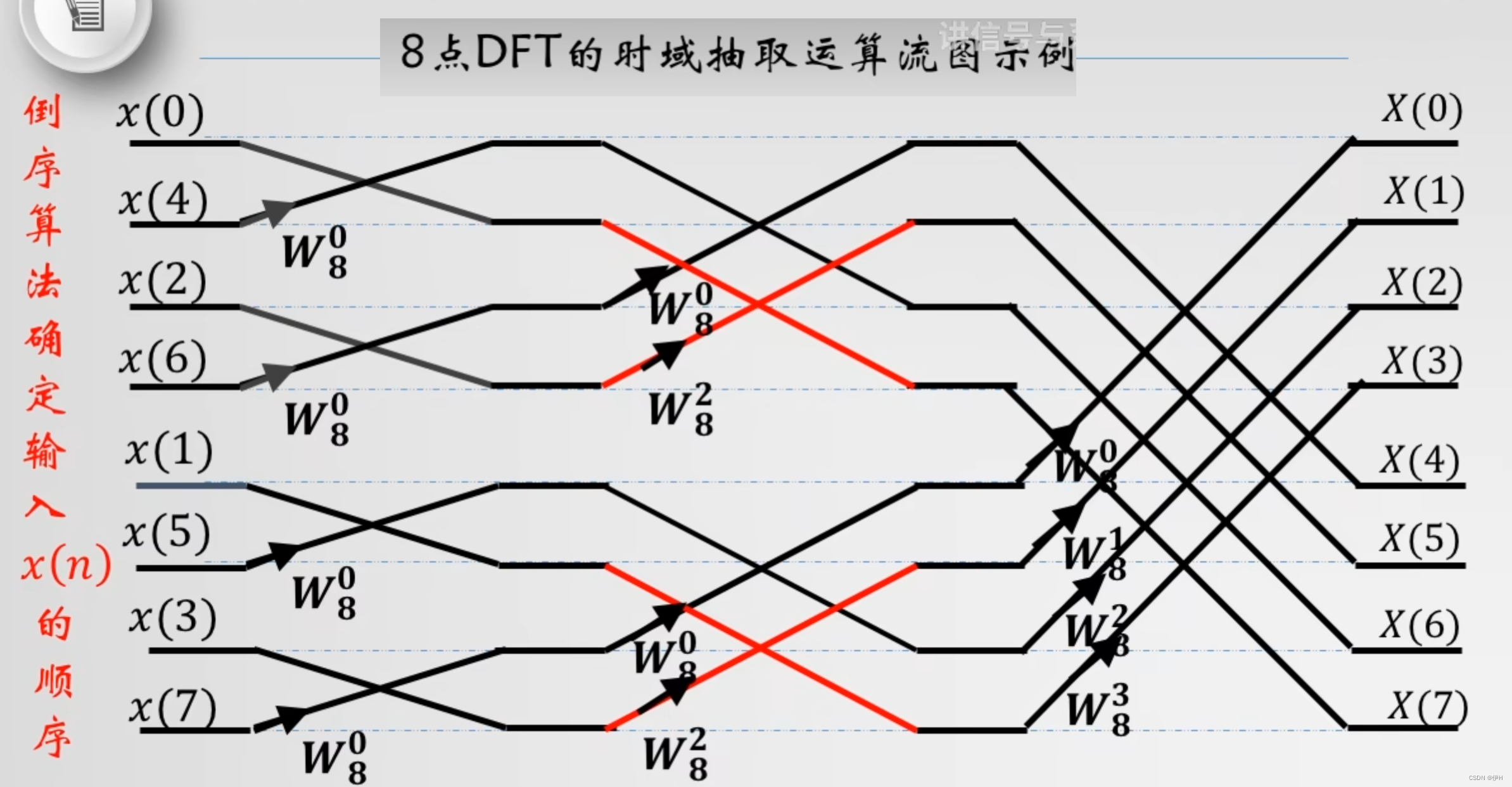
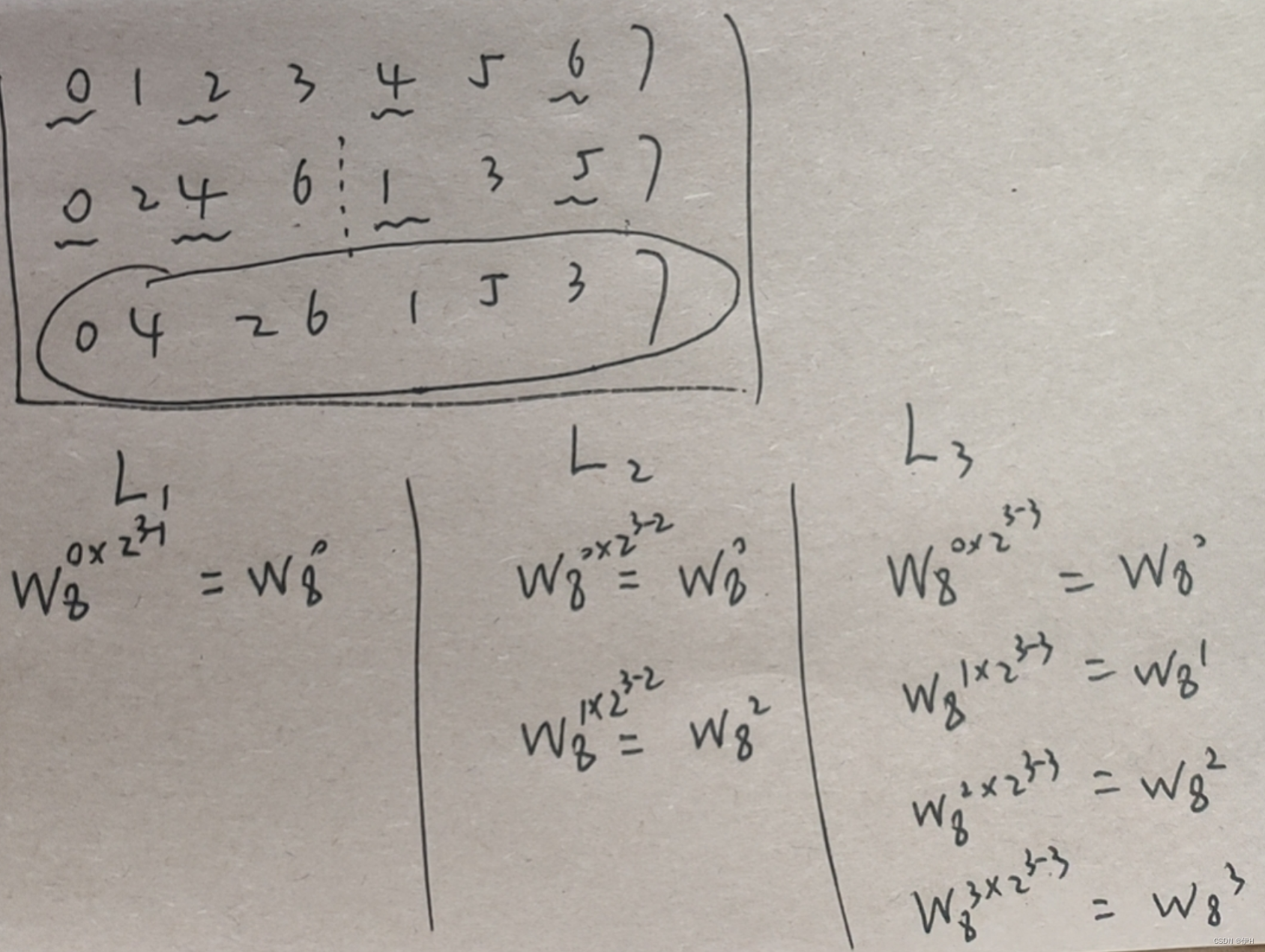
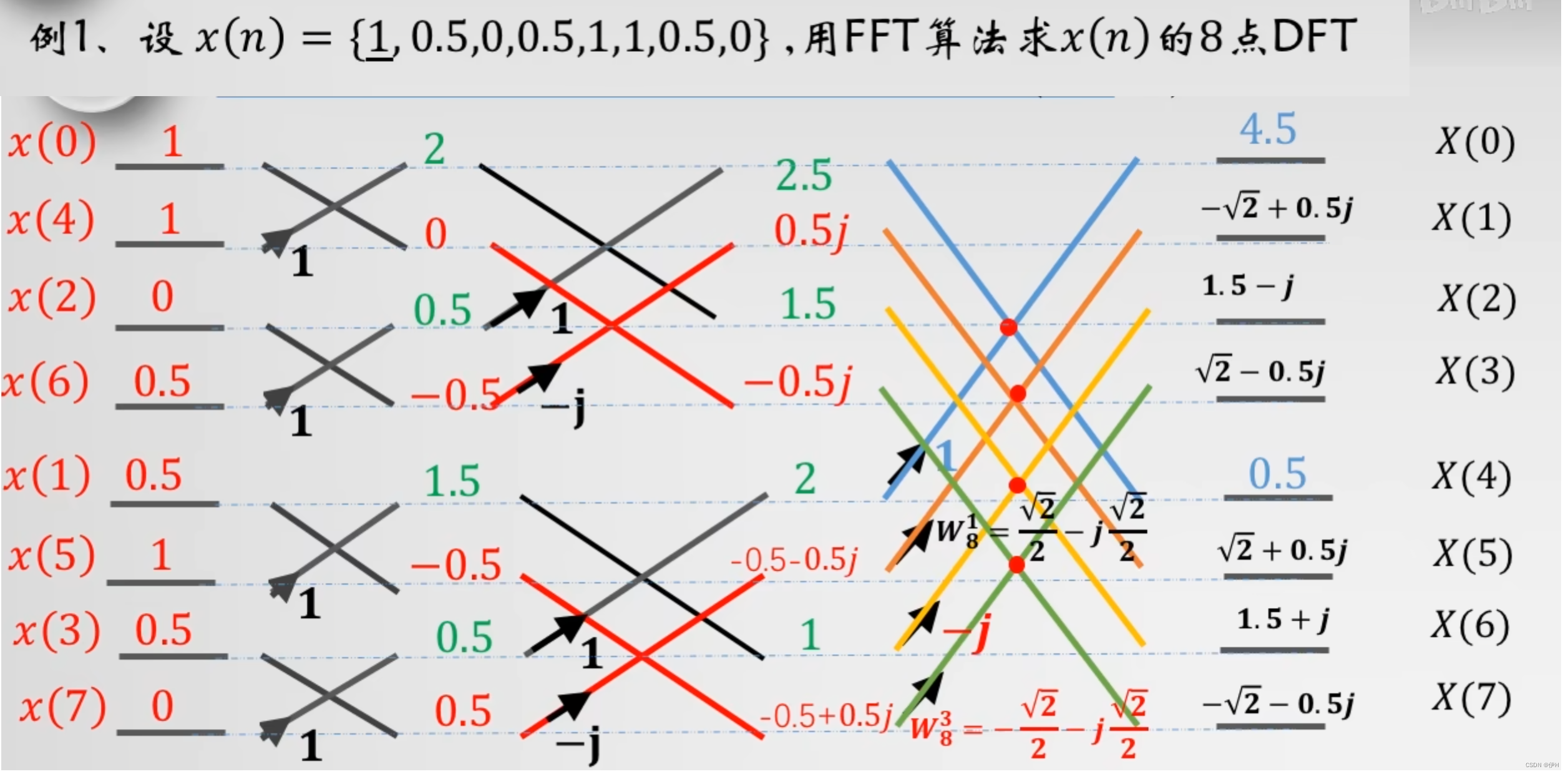
Stockham FFT
以8*8为例子 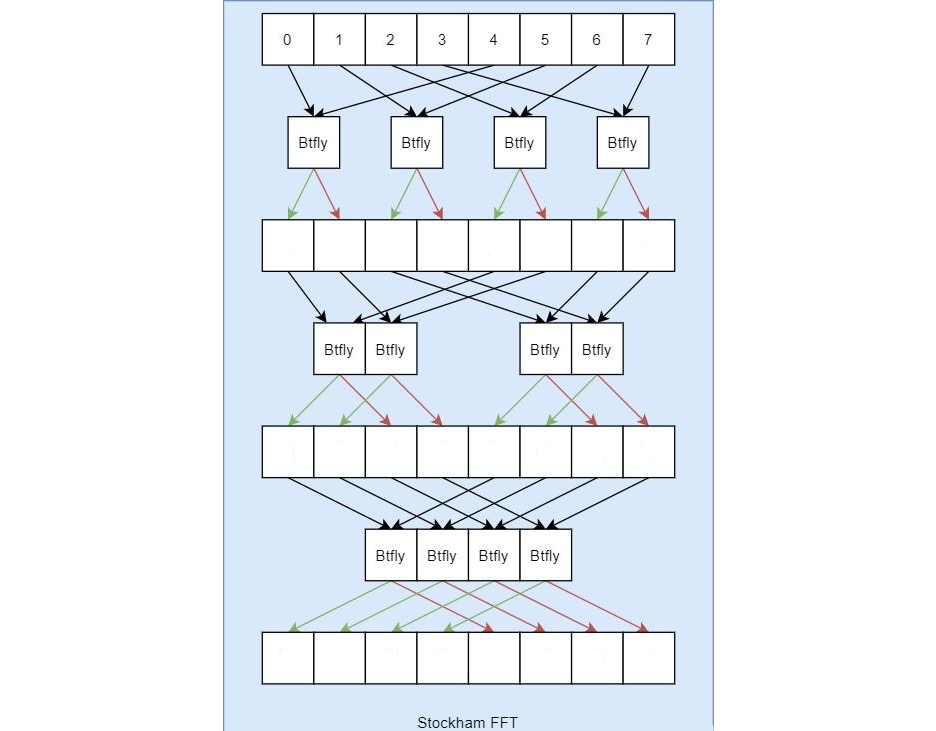
javascript
/**
W_8_0 = 1 + 0i
W_8_1 = 0.7071 - 0.7071i
W_8_2 = 0 - i
W_8_3 = -0.7071 - 0.7071i
*/
/**
是每一次的输出,都是下一次的输入。
*/
/**
第一轮 ☆☆☆☆☆☆☆☆
输入:[0, 1, 2, 3, 4, 5, 6, 7]
W_8_0 = 1
[
0 + (4 * 1 + 4 * 0i), => 4
0 - (4 * 1 + 4 * 0i), => -4
1 + (5 * 1 + 5 * 0i), => 6
1 - (5 * 1 + 5 * 0i), => -4
2 + (6 * 1 + 6 * 0i), => 8
2 - (6 * 1 + 6 * 0i), => -4
3 + (7 * 1 + 7 * 0i), => 10
3 - (7 * 1 + 7 * 0i), => -4
]
输出:[4, -4, 6, -4, 8, -4, 10, -4]
---------------------------------------------------------
第二轮 ☆☆☆☆☆☆☆☆
输入:[4, -4, 6, -4, 8, -4, 10, -4]
W_8_0 = 1 + 0i
W_8_2 = 0 - i
[
4 + (8 * 1 + 8 * 0i), => 12
-4 + (-4 * 0 + -4 * (-i)) => -4 + 4i
4 - (8 * 1 + 8 * 0i), => -4
-4 - (-4 * 0 + -4 * (-i)) => -4 - 4i
6 + (10 * 1 + 10 * 0i) => 16
-4 + (-4 * 0 + -4 * (-i)) => -4 + 4i
6 - (10 * 1 + 10 * 0i) => -4
-4 - (-4 * 0 + -4 * (-i)) => -4 - 4i
]
输出:[12, -4 + 4i, -4, -4 - 4i, 16, -4 + 4i, -4 -4 - 4i]
---------------------------------------------------------
第三轮 ☆☆☆☆☆☆☆☆
输入:[12, -4 + 4i, -4, -4 - 4i, 16, -4 + 4i, -4, -4 - 4i]
W_8_0 = 1 + 0i
W_8_1 = 0.7071 - 0.7071i
W_8_2 = 0 - i
W_8_3 = -0.7071 - 0.7071i
[
0、 12 + (16 * 1 + 16 * 0i)
= 28 + 0i
1、 -4 + 4i + ((-4 + 4i) * 0.7071 + (-4 + 4i) * -0.7071i)
= -4 + 4i -2.8284 + 2.8284i + 2.8284i + 2.8284
= -4 + 9.6568i
2、 -4 + ((-4) * 0 + (-4) * -i)
= -4 + 4i
3、 -4 - 4i + ((-4 - 4i) * -0.7071 + (-4 - 4i) * - 0.7071i)
= -4 - 4i + 2.8284 + 2.8284i + 2.8284i - 2.8284
= -4 + 1.6568i
4、 12 - (16 * 1 + 16 * 0i)
= -4 + 0i
5、 -4 + 4i - ((-4 + 4i) * 0.7071 + (-4 + 4i) * -0.7071i)
= -4 + 4i + 2.8284 - 2.8284i -2.8284i - 2.8284
= -4 - 1.6568i
6、 -4 - ((-4) * 0 + (-4) * -i)
= -4 - 4i
7、 -4 - 4i - ((-4 - 4i) * -0.7071 + (-4 - 4i) * - 0.7071i)
= -4 - 4i - (2.8284 + 2.8284i + 2.8284i - 2.8284)
= -4 - 4i - 5.6568i
= -4 - 9.6568i
]
输出:[
28 + 0i,
-4 + 9.6568i,
-4 + 4i,
-4 + 1.6568i,
-4 + 0i,
-4 - 1.6568i,
-4 - 4i,
-4 - 9.6568i
]
至此,和下面的 python 运算结果一致。
*/javascript
// http://www.fun-ai.org.cn/scratch/python/
import numpy as np
x = np.array([0, 1, 2, 3, 4, 5, 6, 7], dtype=np.complex128) # 显式使用复数类型
theoretical_result = np.fft.fft(x)
print("Theoretical FFT:", theoretical_result)
// Theoretical FFT: [
// 28.+0.j,
// -4.+9.65685425j,
// -4.+4.j,
// -4.+1.65685425j,
// -4.+0.j,
// -4.-1.65685425j,
// -4.-4.j,
// -4.-9.65685425j
// ]输出的下标
每一轮中,循环的次数都是4(即n*k=4)。
输出下标的公式是:
(x - u) * 2 + u
x 是第几个蝶形变换,x ∈ 0,1,2,3。
u 是 x mod 2^m , m ∈ 0,1,2
这个算法为什么这样,看 https://zhuanlan.zhihu.com/p/208511211 【详尽的快速傅里叶变换推导】
第一轮
- m=0、n=4、k=1
- n=4 是因为 blockNum=4
- k=1 是因为 blockSize=2,所以 k=blockSize/2=1
- m=0、n=4、k=1
第二轮
- m=1、n=2、k=2
- n=2 是因为 blockNum=2
- k=2 是因为 blockSize=4,所以 k=blockSize/2=2
- m=1、n=2、k=2
第三轮
- m=2、n=1、k=4
- n=1 是因为 blockNum=1
- k=4 是因为 blockSize=8,所以 k=blockSize/2=4
- m=2、n=1、k=4
javascript
var tempArray = OutputData
var logRes = log2(8) // 即 3
for (var m = 0; m < logRes; m ++) {
var indexIn = 0
var step = 2^m // 即:1,2,4。这个是间隔步长。
var blockSize = 2^(m+1) // 即:2,4,8。
var blockNum = 8 / blockSize // 即:4,2,1。一共有多少块需要循环。
var kFor = blockSize / 2 // 即:1,2,4。每个块需要循环从次数。
for (var n = 0; n < blockNum; n ++) {
for (var k = 0; k < kFor; k ++) {
var inputData1 = OutputData[indexIn]
var inputData2 = OutputData[indexIn + 4]
var outputIndex1 = 2 * (indexIn - (indexIn mod 2^m)) + (indexIn mod 2^m)
var outputIndex2 = outputIndex1 + step
var indexW = k * 2^(logRes - (m + 1))
var w = dataW[indexW]
var p1 = inputData1
var p2 = 复数乘法(inputData2, w)
tempArray[outputIndex1] = p1 + p2
tempArray[outputIndex2] = p1 - p2
indexIn ++
}
}
OutputData = tempArray
}javascript
function complexMultiply(a, b) {
return {
x: a.x * b.x - a.y * b.y, // 实部
y: a.x * b.y + a.y * b.x // 虚部
}
}
function complexAdd(a, b) {
return {
x: a.x + b.x, // 实部
y: a.y + b.y // 虚部
}
}
function complexSubtraction(a, b) {
return {
x: a.x - b.x, // 实部
y: a.y - b.y // 虚部
}
}
let OutputData = [
{ x: 0, y: 0 },
{ x: 1, y: 0 },
{ x: 2, y: 0 },
{ x: 3, y: 0 },
{ x: 4, y: 0 },
{ x: 5, y: 0 },
{ x: 6, y: 0 },
{ x: 7, y: 0 },
]
let tempArray = new Array(8)
const dataW = [
{ x: 1, y: 0 },
{ x: 0.7071, y: -0.7071 },
{ x: 0, y: -1 },
{ x: -0.7071, y: -0.7071 },
]
const logRes = 3
for (var m = 0; m < logRes; m++) {
var indexIn = 0
var step = Math.pow(2, m)
var blockSize = Math.pow(2, m + 1)
var blockNum = 8 / blockSize
var kFor = blockSize / 2
for (var n = 0; n < blockNum; n++) {
for (var k = 0; k < kFor; k++) {
var inputData1 = OutputData[indexIn]
var inputData2 = OutputData[indexIn + 4]
var outputIndex1 = 2 * (indexIn - (indexIn % Math.pow(2, m))) + (indexIn % Math.pow(2, m))
var outputIndex2 = outputIndex1 + step
var indexW = k * Math.pow(2, 3 - (m + 1))
var w = dataW[indexW]
var p1 = inputData1
var p2 = complexMultiply(inputData2, w)
tempArray[outputIndex1] = complexAdd(p1, p2)
tempArray[outputIndex2] = complexSubtraction(p1, p2)
indexIn++
}
}
OutputData = tempArray
tempArray = []
}
console.log(OutputData)
// [
// {
// "x": 28,
// "y": 0
// },
// {
// "x": -4,
// "y": 9.6568
// },
// {
// "x": -4,
// "y": 4
// },
// {
// "x": -4,
// "y": 1.6567999999999996
// },
// {
// "x": -4,
// "y": 0
// },
// {
// "x": -4,
// "y": -1.6567999999999996
// },
// {
// "x": -4,
// "y": -4
// },
// {
// "x": -4,
// "y": -9.6568
// }
// ]javascript
let list = []
function complexMultiply(a, b) {
return {
x: a.x * b.x - a.y * b.y, // 实部
y: a.x * b.y + a.y * b.x // 虚部
}
}
function complexAdd(a, b) {
return {
x: a.x + b.x, // 实部
y: a.y + b.y // 虚部
}
}
function complexSubtraction(a, b) {
return {
x: a.x - b.x, // 实部
y: a.y - b.y // 虚部
}
}
list = [
18.981624193185777,
21.72065757030428,
16.447474387356934,
22.993932387133217,
18.106364793791336,
13.05106293427047,
15.893983477237896,
19.42478727038987,
17.166599707321495,
9.866400314345183,
7.59787385910128,
14.567197303499817,
14.70930597077771,
7.896936476775536,
12.900951861540339,
7.4406024047751345,
18.981624193185777,
21.72065757030428,
16.447474387356934,
22.993932387133217,
18.106364793791336,
13.05106293427047,
15.893983477237896,
19.42478727038987,
17.166599707321495,
9.866400314345183,
7.59787385910128,
14.567197303499817,
14.70930597077771,
7.896936476775536,
12.900951861540339,
7.4406024047751345
]
let size = list.length
let OutputData = []
let logRes = Math.log2(size)
let tempArray = new Array(size)
let dataW = []
let half = size / 2
for (let i = 0; i < size; i++) {
OutputData.push({
x: list[i],
y: 0
})
let angle = (2 * Math.PI * i) / size
let rePositiveInverse = Math.cos(angle)
let imPositiveInverse = -Math.sin(angle)
dataW.push({
x: rePositiveInverse,
y: imPositiveInverse
})
}
for (var m = 0; m < logRes; m++) {
var indexIn = 0
var step = 1 << m
var blockSize = 1 << (m + 1)
var blockNum = size / blockSize
var kFor = blockSize / 2
for (var n = 0; n < blockNum; n++) {
for (var k = 0; k < kFor; k++) {
var inputData1 = OutputData[indexIn]
var inputData2 = OutputData[indexIn + half]
var outputIndex1 = 2 * (indexIn - (indexIn % Math.pow(2, m))) + (indexIn % Math.pow(2, m))
var outputIndex2 = outputIndex1 + step
var indexW = k * (1 << (logRes - m - 1))
var w = dataW[indexW]
var p1 = inputData1
var p2 = complexMultiply(inputData2, w)
tempArray[outputIndex1] = complexAdd(p1, p2)
tempArray[outputIndex2] = complexSubtraction(p1, p2)
indexIn++
}
}
OutputData = []
for(let i =0 ;i<size;i++){
OutputData.push({...tempArray[i]})
}
tempArray = []
}
console.log(OutputData)逆fft算法
javascript
// 逆fft需要修改
// 1、旋转因子
// 2、归一化,即for (let i = 0; i < size; i++) { OutputData[i].x /= size; OutputData[i].y /= size; }
let list = []
function complexMultiply(a, b) {
return {
x: a.x * b.x - a.y * b.y, // 实部
y: a.x * b.y + a.y * b.x // 虚部
}
}
function complexAdd(a, b) {
return {
x: a.x + b.x, // 实部
y: a.y + b.y // 虚部
}
}
function complexSubtraction(a, b) {
return {
x: a.x - b.x, // 实部
y: a.y - b.y // 虚部
}
}
list = [
18.981624193185777,
21.72065757030428,
16.447474387356934,
22.993932387133217,
18.106364793791336,
13.05106293427047,
15.893983477237896,
19.42478727038987,
17.166599707321495,
9.866400314345183,
7.59787385910128,
14.567197303499817,
14.70930597077771,
7.896936476775536,
12.900951861540339,
7.4406024047751345,
18.981624193185777,
21.72065757030428,
16.447474387356934,
22.993932387133217,
18.106364793791336,
13.05106293427047,
15.893983477237896,
19.42478727038987,
17.166599707321495,
9.866400314345183,
7.59787385910128,
14.567197303499817,
14.70930597077771,
7.896936476775536,
12.900951861540339,
7.4406024047751345
]
let size = list.length
let OutputData = []
let logRes = Math.log2(size)
let tempArray = new Array(size)
let dataW = []
let half = size / 2
for (let i = 0; i < size; i++) {
OutputData.push({
x: list[i],
y: 0
})
let angle = (2 * Math.PI * i) / size
let rePositiveInverse = Math.cos(angle)
let imPositiveInverse = Math.sin(angle)
dataW.push({
x: rePositiveInverse,
y: imPositiveInverse
})
}
for (var m = 0; m < logRes; m++) {
var indexIn = 0
var step = 1 << m
var blockSize = 1 << (m + 1)
var blockNum = size / blockSize
var kFor = blockSize / 2
for (var n = 0; n < blockNum; n++) {
for (var k = 0; k < kFor; k++) {
var inputData1 = OutputData[indexIn]
var inputData2 = OutputData[indexIn + half]
var outputIndex1 = 2 * (indexIn - (indexIn % Math.pow(2, m))) + (indexIn % Math.pow(2, m))
var outputIndex2 = outputIndex1 + step
var indexW = k * (1 << (logRes - m - 1))
var w = dataW[indexW]
var p1 = inputData1
var p2 = complexMultiply(inputData2, w)
tempArray[outputIndex1] = complexAdd(p1, p2)
tempArray[outputIndex2] = complexSubtraction(p1, p2)
indexIn++
}
}
OutputData = []
for(let i =0 ;i<size;i++){
OutputData.push({...tempArray[i]})
}
tempArray = []
}
// 在最终输出前加入归一化操作
for (let i = 0; i < size; i++) {
OutputData[i].x /= size;
OutputData[i].y /= size; // 如果只需要实部结果,可以保留 x,将 y 置为零
}
console.log(OutputData)